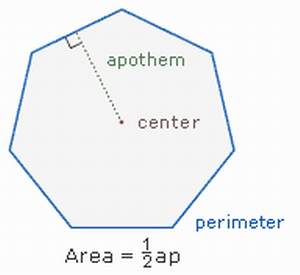
รูปหลายเหลี่ยม (Polygon)

         รูปหลายเหลี่ยม (Polygon)  คือ รูปบนระนาบที่มีด้านทุกด้านเป็นเส้นตรง ถ้าด้านทุกด้านเท่ากันเราเรียกว่า รูปหลายเหลี่ยมด้านเท่า รูป หลายเหลี่ยมที่มีจำนวนด้านน้อยที่สุดคือรูปสามเหลี่ยม ซึ่งมีด้านเป็นเส้น ตรงเพียงสามด้านเท่านั้น เราอาจจะแบ่งรูปสามเหลี่ยม ตามลักษณะของมุมและด้านของรูปได้ 6 แบบ คือ

        1. รูปสามเหลี่ยมมุมฉากจะมีมุมๆ หนึ่งเท่ากับ 90 องศา เมื่อเอาสามเหลี่ยมมุมฉากที่เท่ากันสองรูป มาวางให้ด้านที่อยู่ตรงข้าม มุมฉากประกบกันสนิท (ตามรูป) จะได้รูปสี่เหลี่ยมผืนผ้าหนึ่งรูปพอดีแสดงว่ารูปสามเหลี่ยมมุมฉากมีพื้นที่ เท่ากับครึ่งหนึ่งของรูปสี่เหลี่ยมผืนผ้า

   ดังนั้น พื้นที่สามเหลี่ยมมุมฉาก  = 1/2 x ฐาน x สูง

2. สามเหลี่ยมมุมแหลม  มีมุมทั้งสามเล็กกว่า 90  องศา

3. สามเหลี่ยมมุมป้าน  มีมุมหนึ่งมุมใหญ่กว่า 90  องศา

4. สามเหลี่ยมด้านเท่า มีด้านทั้งสามยาวเท่ากัน  มุมภายในของสามเหลี่ยมด้านเท่าต่างเท่ากับ  60  องศาทุกมุม

5. สามเหลี่ยมหน้าจั่ว เป็นรูปสามเหลี่ยมที่มีด้านสองด้านยาวเท่ากัน หน้าจั่ว ของบ้านแบบไทย หน้าจั่วของโบสถ์วิหารหรือศาลา ล้วนมีลักษณะเป็นรูปสาม เหลี่ยมหน้าจั่วทั้งนั้น

6. สามเหลี่ยมด้านไม่เท่า  ด้านทั้งสามมีความยาวไม่เท่ากัน

สามเหลี่ยมอยู่บนฐานเดียวกันและมีความสูงเท่ากันจะมีพื้นที่เท่ากัน เสมอ เพราะต่างก็มีพื้นที่เป็นครึ่งหนึ่งของสี่เหลี่ยมผืนผ้าซึ่งมีฐานเดียว กันและมีความสูงเท่ากัน

สูตร

การหาพื้นที่ของรูปสามเหลี่ยมทั่วไปก็คือ พื้นที่ของรูปสามเหลี่ยม  = 1/2 x ฐาน x สูง

ถ้า a, b และ c แทนความยาวของด้านทั้งสามของรูปสามเหลี่ยมและ 2 s แทนความยาวของเส้นรอบรูปของรูปสามเหลี่ยม กล่าวคือ 2s = a + b + c เราอาจจะหาพื้นที่ของรูปสามเหลี่ยมได้จาก

สูตร

        พื้นที่ของรูปสามเหลี่ยม   =   s(s-a)(s-b)(s-c)

จากวิชาตรีโกณมิติ พื้นที่ของรูปสามเหลี่ยมมีความสัมพันธ์กับด้านและมุมของ สามเหลี่ยมนั้น เช่น เมื่อทราบความยาวของด้านสองด้านและขนาดของมุมที่อยู่ ระหว่างด้านทั้งสอง เราจะได้พื้นที่ของรูปสามเหลี่ยมจากสูตร

พื้นที่รูปสามเหลี่ยม = 1/2 bc sin A = 1/2 ca sin B = 1/2 ab sin C

ในเมื่อ a, b, และ c เป็นความยาวของด้านที่อยู่ตรงข้ามกับมุม A, B และ C ตามลำดับ

ที่จริงแล้วถ้าเราทราบค่าของด้านและมุมของรูปสามเหลี่ยมเพียง 3 ค่าเท่านั้น เราก็อาจจะคำนวณหาค่าที่เหลืออีก 3  ค่า รวมทั้งค่าของพื้นที่ของรูปสามเหลี่ยมนั้นได้เสมอ  นักสำรวจรังวัดได้นำความรู้นี้ไปใช้ในการหาพื้นที่ของที่ดินที่มีลักษณะ ต่างๆ โดยแบ่งที่ดินนั้นออกเป็นรูปสามเหลี่ยมหลายรูป วัดด้านและมุมของสามเหลี่ยม ทุกรูปที่ได้ ก็จะสามารถคำนวณหาพื้นที่ของรูปสามเหลี่ยมทุกรูปได้ เมื่อรวมผลลัพธ์ทั้งหมดก็จะได้ขนาดของพื้นที่ที่รังวัดนั้น

ที่มา :  http://www.kroobannok.com 

By  :  http://www.physics2u.org/index.php?option=com

คณิตศาสตร์ในชีวิตประจำวัน

การประยุกต์คณิตศาสตร์ไปใช้ในชีวิตประจำวัน 

             คณิตศาสตร์ในชีวิตประจำวัน หมาย ถึงการนำความรู้ เนื้อหา หลักการทางคณิตศาสตร์ ในระดับที่เหมาะสมกับผู้เรียน ไปประยุกต์ใช้ในกิจกรรมที่เกี่ยวข้องกับผู้เรียน หรือใช้อธิบายปรากฏการณ์ เหตุการณ์ใกล้ตัวที่สามารถพบเห็นได้ในชีวิตประจำวันทั่วไป ทุก เหตุการณ์ที่เกิดขึ้นกับเรา ไม่ว่าจะเกิดขึ้นทุกวันหรือนานๆ ครั้ง ทั้งที่เกี่ยวข้องกับเราโดยตรงหรือโดยอ้อม ล้วนแต่สามารถโยงให้เข้ากับคณิตศาสตร์ได้ทั้งสิ้น ในชีวิตประจำวันทุกคนจึงต้องได้ใช้คณิตศาสตร์ ใช้ทั้งที่รู้ตัวและไม่รู้ตัว คณิตศาสตร์ในชีวิตประจำวันจึงไม่ได้มีความหมายด้อยค่าเพียงแค่การบวก ลบ คูณ หาร การซื้อขาย ทอนเงิน ส่วนลด หรือการมองเห็นวัตถุเหลี่ยมๆ กลมๆ แล้วพึงใจว่านี้คือรูปเรขาคณิต และขณะเดียวกันก็ไม่ได้หมายว่าคณิตศาสตร์ในชีวิตประจำวันจะต้องเป็นเฉพาะ คณิตศาสตร์ที่ยาก หรือคณิตศาสตร์ชั้นสูงที่มีส่วนสำคัญในการพัฒนาวิทยาศาสตร์และเทคโนโลยีล้ำ สมัยเท่านั้น เนื่องจากชีวิตประจำวันของแต่ละคนต่างกัน ชีวิตประจำวันของนักเรียน ครู นักวิทยาศาสตร์ และประชาชนทั่วไปจึงย่อมแตกต่างกันด้วย หลักสำคัญของ ”คณิตศาสตร์ในชีวิตประจำวัน” จึงอยู่ที่มุมมองในการนำคณิตศาสตร์ไปประยุกต์ใช้หรือใช้อธิบายเหตุการณ์ใกล้ ตัว เหตุการณ์ที่สนใจ ซึ่งสามารถพบเห็นได้ในชีวิตประจำวันทั่วไป “คณิตศาสตร์ในชีวิตประจำวัน” จึงเป็นเสมือนสะพานที่เชื่อมระหว่างคณิตศาสตร์กับชีวิตจริง ทำให้คณิตศาสตร์หลุดพ้นจากโลกที่เป็นนามธรรม มาสู่โลกที่เป็นรูปธรรม ทำให้คณิตศาสตร์เป็นเรื่องใกล้ตัว จับต้องได้ และใช้งานได้จริง ซึ่งจะทำให้ผู้เรียนได้ตระหนักถึงความสำคัญของคณิตศาสตร์ และมีเจตคติที่ดีต่อวิชาคณิตศาสตร์
By :  http://noyna-narumon.blogspot.com/p/blog-page_05.html